In this paper, we look at the representation of concepts in machine learning models. Concepts can be defined abstractly and ontologically, however, we utilise more of a working definition in this paper that depends on the machine learning model under consideration.

A concept is an idea that can be explicitly identified in a set of compatible inputs to the model and explicitly not identified in a distinct set of compatible inputs.

This definition is influenced by prior work on concept activation vectors. These are a vector representation of concepts in the latent space of machine learning models, constructed by training a linear classifier to distinguish between the set of inputs referenced in the definition.

The intuition here is that the classifier, to perform well, understands the relationship between inputs with the concept and inputs without the concept. Therefore, characterising the linear classifier with the canonical orthogonal vector to its decision boundary provides a concept vector that points in the direction of inputs with the concept present to inputs where the concept is not present.

On the one hand, it is shown that concept activation vectors do capture something meaningful, in particular about its relationship to other concepts. On the other hand, it can be sensitive to the initialisation of the classifier and it does not capture the concept to the fullest extent. A reason these issues arise is that typically many classifiers perform well at distinguishing these sets of input data, but provide different concept vectors.

Our motivation was to construct a more robust vector representation of a concept, by working under the hypothesis that the geometry of the boundary between these sets of input data captures significant semantic details. We propose to construct the concept vector representation as the vector most aligned with the so-called boundary normal vectors. These are the vectors connecting points along the boundary of the sets of data, and in our paper, we provide an algorithm to determine these.

We term these concept vectors as concept boundary vectors and find that they outperform concept activation vectors on many of the benchmarks previously used to evaluate these representations. This supports the hypothesis that the geometry of the boundary between sets of data is paramount in encoding the relationship between the sets of data.

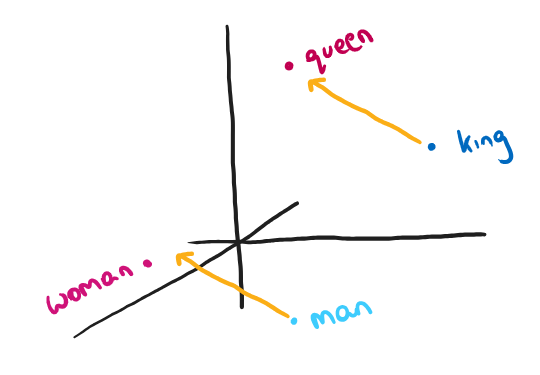
Of particular interest, was our observation that concept boundary vectors are more faithful to the previously observed linearity of concept relationships. In traditional embedding models, such as Word2Vec, it was observed that relationships between concepts were approximately linear. For instance, if I added the vector going from "king" to "queen" to the vector of "man", I would arrive somewhere near "woman". Suggesting that there is a male-to-female direction in the model's representation. Concept boundary vectors are more aligned with this direction than concept activation vectors.

We hope concept boundary vectors provide a better mechanism to explore the inside of machine learning models.