Abstract

A key challenge for the machine learning community is to understand and accelerate the training dynamics of deep networks that lead to delayed generalisation and emergent robustness to input perturbations, also known as grokking. Prior work has associated phenomena like delayed generalisation with the transition of a deep network from a linear to a feature learning regime, and emergent robustness with changes to the network's functional geometry, in particular the arrangement of the so-called linear regions in deep networks employing continuous piecewise affine nonlinearities. Here, we explain how grokking is realised in the Jacobian of a deep network and demonstrate that aligning a network's Jacobians with the training data (in the sense of cosine similarity) ensures grokking under a low-rank Jacobian assumption. Our results provide a strong theoretical motivation for the use of Jacobian regularisation in optimizing deep networks -- a method we introduce as GrokAlign -- which we show empirically to induce grokking much sooner than more conventional regularizers like weight decay. Moreover, we introduce centroid alignment as a tractable and interpretable simplification of Jacobian alignment that effectively identifies and tracks the stages of deep network training dynamics.

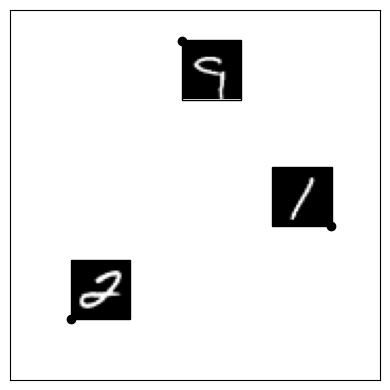
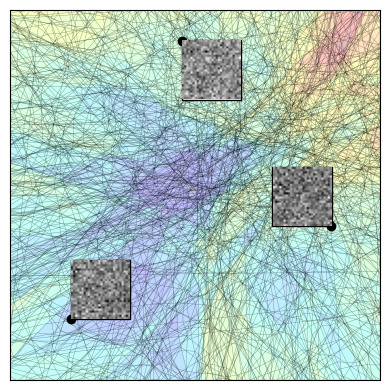
Fig: For deep networks to grok, their Jacobians should align such that the sum of their rows is cosine-similar to the point at which they were computed; we dub this condition centroid aligned. This has consequences on the functional geometry of deep networks through the Spline Theory of Deep Learning. Here we train a ReLU network on the MNIST dataset using GrokAlign, which is a method for regularising the Jacobian matrices of a deep network during training. We take three training data points, left, and observe the linear regions (using SplineCam) of the deep network along with the centroids of the three data points when it has memorized the training data, centre, and when it has generalised, right. We colour the linear regions according to the norm of the linear operator acting upon them.

Jacobian and Centroid Alignment

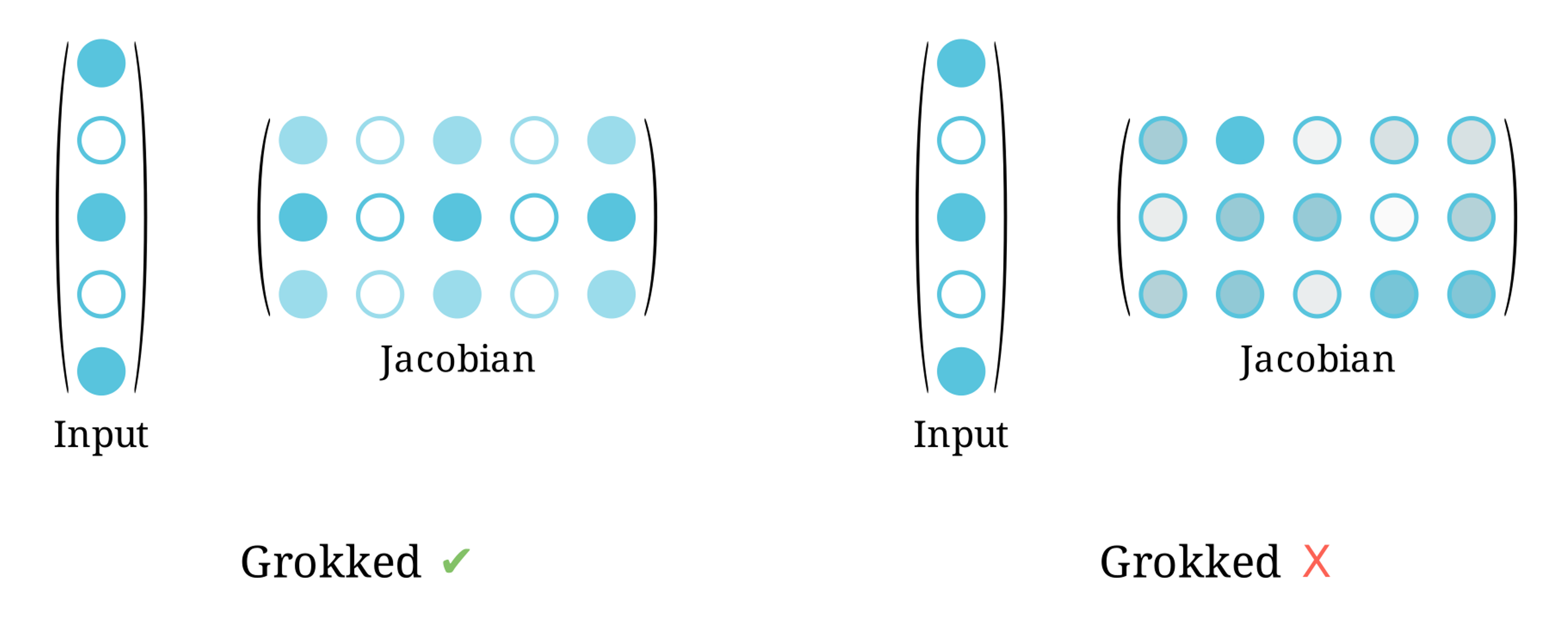
Definition: A deep network is Jacobian-aligned at point if its rows are scalar multiples of that point.

Jacobian aligned deep networks optimize the training objective on a constrained set.

Jacobian aligned deep networks are optimally robust on local regions of the input space.

Definition: A centroid at a point is equal to the sum of the rows of the Jacobian.

Centroids parametrise the functional geometry of deep networks.

Proposition: Jacobian alignment implies centroid alignment.

Centroid alignment identifies the feature learning of deep networks.

Centroid alignment efficiently captures the training dynamics of deep networks.

Centroid Alignment Identifies Feature Learning

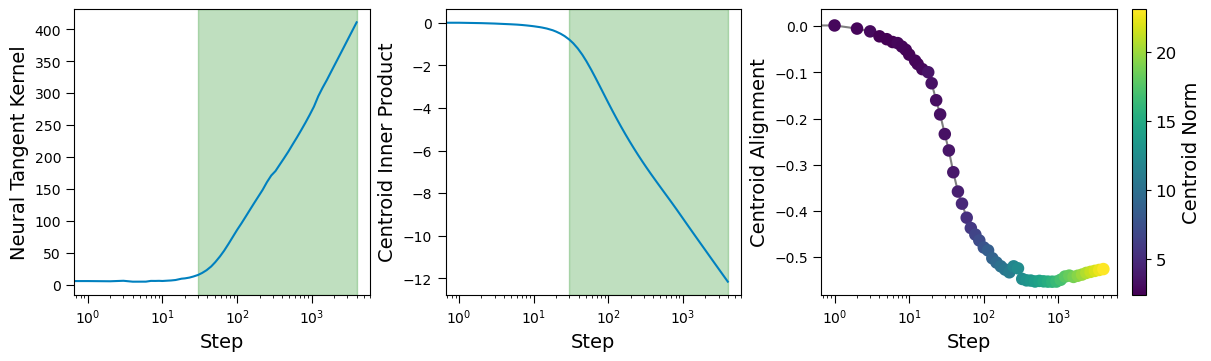
Fig: Using the neural tangent kernel, we demonstrate theoretically that a changing inner product between a centroid and the point it was computed at represents the feature learning regime of deep network training; when translated into a changing alignment we see the generalisation of a deep networks learned representations. Here we train a two-layer scalar-output ReLU network to distinguish between the zero and one class of the MNIST dataset. For a point in the training set we monitor the inner product and alignment (cosine similarity) to its corresponding centroid, which is computed efficiently through a Jacobian vector product. By also monitoring the neural tangent kernel, we support our theoretical conclusion that a changing inner product corresponds to the feature learning regime of training. Furthermore, we note that the factor inhibiting centroid alignment, which is an artefact of an optimal deep network, is the norm of the centroid.

Centroid Alignment Identifies Robustness

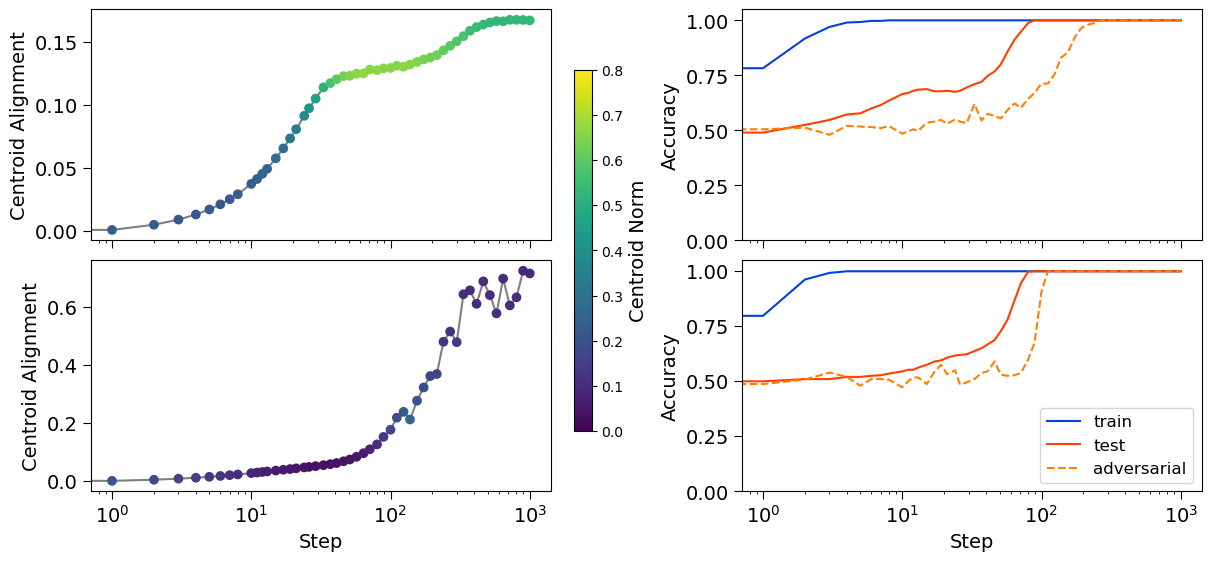
Fig: Since Jacobian alignment is a necessary condition for deep network robustness under a low-rank Jacobian assumption, it follows that centroid alignment is a artifact of a robustness deep network. Here we demonstrate that a higher centroid alignment corresponds to a more robust deep network. More specifically, we consider the XOR grokking set up of Xu et al. (2025) and monitor the centroid alignment and robustness of the deep network through training. In the top row we use weight-decay, whereas in the bottom row we also use GrokAlign. We see that by using GrokAlign, the norm of the centroid is maintained at a relatively lower value allowing it to become aligned which correlates with the accelerate onset of robustness.

GrokAlign Induces Alignment and Thus Accelerates Grokking

GrokAlign is our solution to the observation that standard deep network training techniques do not maintain a low Jacobian norm which inhibits their alignment and thus grokking. GrokAlign regularises the Frobenius norms of the Jacobians of a deep network on the training data during training by appending their values to the loss function with some weighting coefficient.

Fig: Using GrokAlign significantly accelerates the rate of grokking. In our paper we perform a study which determines this speed up factor can be up to 7 times faster. We assume the MNIST grokking set up of Liu et al.(2022) in the top row, and we additionally utilise GrokAlign in the bottom row. Clearly, grokking occurs earlier in the model trained with GrokAlign. To the right of each accuracy plot we visualise the centroid of a point from the training set. We observe that during the grokking phase the centroid develops a structure which under GrokAlign is more resemblant of the training point, this is centroid alignment.

Citation