Implicit neural representations are formed using deep network architectures trained to form an internal representation of a particular object, which can then be leverage for inference purposes. For instance, an object may initially be represented as an image, and a deep network may be trained to form a representation of the image which can then be utilised for image augmentation, simulation or graphical modelling.

For simplicity, we will consider the case where we are obtaining a neural representation of a two-dimensional image depicting an object. In this case, the pixel coordinates are inputted into the deep network, that then aims to predict the pixel intensity values. To then obtain the network's representation of the object we can query to model at each pixel coordinate.

Here we investigate the ability of the deep network to form its representation when varying amounts of the initial image data is discarded from the training data. We do this by measuring the faithfulness of the implicit representations boundary to the actual boundary of the objects in the image. Moreover, we investigate how this ability changes as model capacity changes. In our set up we will take an image, manually identify its boundary and then set the pixel values on the interior to one and pixel values on the exterior to zero. We will then train a deep network to predict these pixel values based on their coordinates. To analytically identify the implicit boundary of the representation we use SplineCam. To then measure the discrepancy between this and the actual boundary of the image we use the Chamfer distance. In our experiments we consider deep networks with four layers of constant widths $[4,8,16,32,64,128]$. We consider these networks trained on the image data at different levels of sparsity by patching the initial image. When performing this patching we only remove points not lying on the boundary so that there is still a signal for the deep network to obtain a representation for the boundary. More specifically, we consider input data where $[0.8,0.9,0.91,0.92,0.93,0.94,0.95,0.96,0.97,0.98,0.99,1.0]$ of the data not lying on the boundary has been patched. For each of these sets of data, and for each of the deep network architectures we train five different instantiations to get an average value of the Chamfer distance between the implicit boundary and the actual boundary.

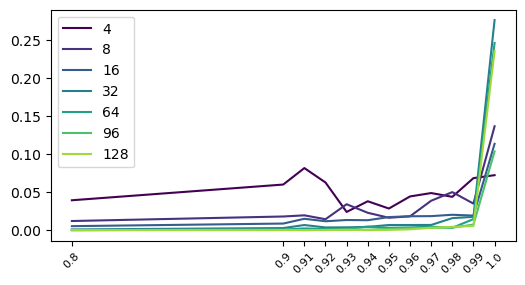
What we observe is that as the capacity of the deep network decreases, the Chamfer distance decrease. This is to be expected, since the lower capacity models will be less able to capture the geometry of the boundary. Similarly, we observe that the Chamfer distance increases as the input data becomes more sparse. Again this is to be expected as, when the data is sparse there is less signal to form a good representation of the boundary. What is perhaps more surprising is that the Chamfer distance actually stays fairly low until only the decision boundary is left. Suggesting that the models need some signal away from the boundary to help form a representation of the boundary.

code