The generalisation property of a neural network is its capacity to transfer good performance on a training set to a test set. On the other hand, a neural network is robust if its outputs are not drastically influenced by perturbations to its inputs.

Intuitively, for me at least, it seems as though these properties of a neural network are inherently linked, if not equivalent. Theoretically, it is shown in [1] that in the limit of dataset size, a learning algorithm generalises if and only if it is robust against perturbations to the inputs.

We can test this intuition by investigating a neural network that undergoes grokking. Grokking is a phenomena first exhibited by neural networks in [2] where it was shown that neural networks can be made to achieve high training accuracy within the initial optimization steps, and then experience an extensive delay before saturating a test set. At a high level grokking can be explained as the transition of a neural network from memorisation to generalisation [3]. Essentially, at the beginning of the optimisation process the neural network is memorising the training set. As the neural network continues to train it slowly replaces this memorisation with a more algorithmic representation of the data. Consequently, its learned representation of the data is more general meaning that it performs well on the test set as well as the training set.

Grokking has subsequently been replicated on neural networks trained on the MNIST dataset after realising that the initialisation and decay of the neural network parameters influences the propensity for grokking [4].

The evolution of training and test discrepancy throughout the training of a neural network offers an opportunity to investigate the relationship between robustness and generalisation. More specifically, to validate the intuition that robustness and generalisation are inherently linked we would expect to observe a grokked network to have low robustness at the beginning of training and a higher robustness once the test accuracy increases.

We can replicate the results of [4], and save the model state when training accuracy first reaches 99% and then again when the validation accuracy increases to above 85%.

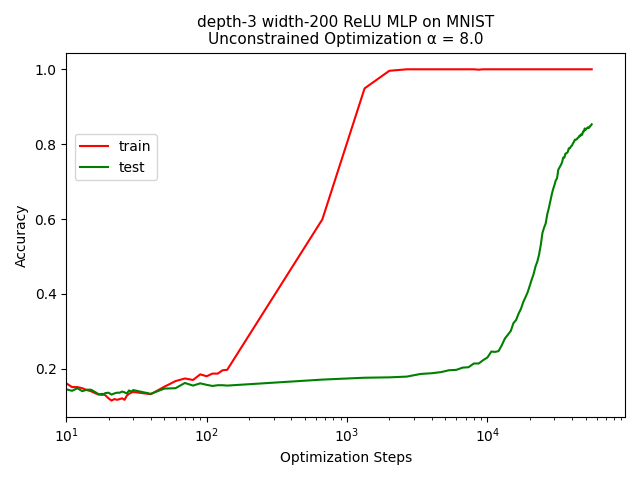
We can then gauge the robustness of these models by determining under what amplitude of perturbation the model cannot correctly classify five randomly perturbed images of that amplitude.

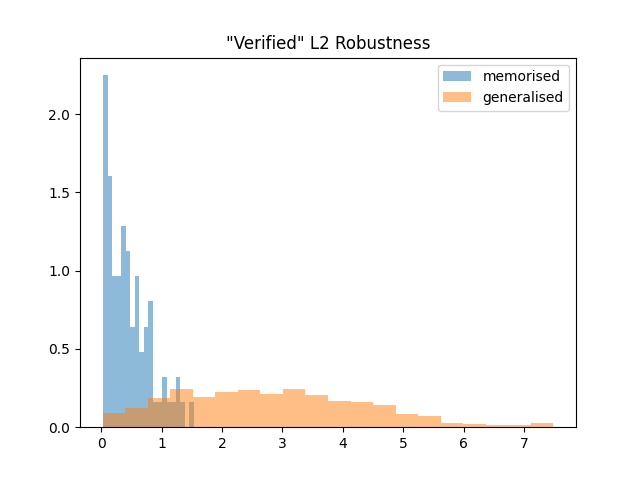
What we observe is that the model obtained from the beginning of the optimisation process is significantly less robust than the model obtained once test accuracy has increased.

Code for these figures can be found here.

References

[1] Xu, Huan, and Shie Mannor. Robustness and Generalization. arXiv:1005.2243, arXiv, 12 May 2010. arXiv.org, http://arxiv.org/abs/1005.2243.

[2] Power, Alethea, et al. Grokking: Generalization Beyond Overfitting on Small Algorithmic Datasets. arXiv:2201.02177, arXiv, 6 Jan. 2022. arXiv.org, http://arxiv.org/abs/2201.02177.

[3] Nanda, Neel, et al. Progress Measures for Grokking via Mechanistic Interpretability. arXiv:2301.05217, arXiv, 19 Oct. 2023. arXiv.org, http://arxiv.org/abs/2301.05217.

[4] Liu, Ziming, et al. Omnigrok: Grokking Beyond Algorithmic Data. arXiv:2210.01117, arXiv, 23 Mar. 2023. arXiv.org, http://arxiv.org/abs/2210.01117.