Neural networks, with ReLU activation functions, are known to be piece-wise linear functions. The neural network is trained to arrange piece-wise linear components to approximate an output distribution.

For neural networks satisfying some assumptions, one can characterise them as operators taking the maximum over a series of linear functions.

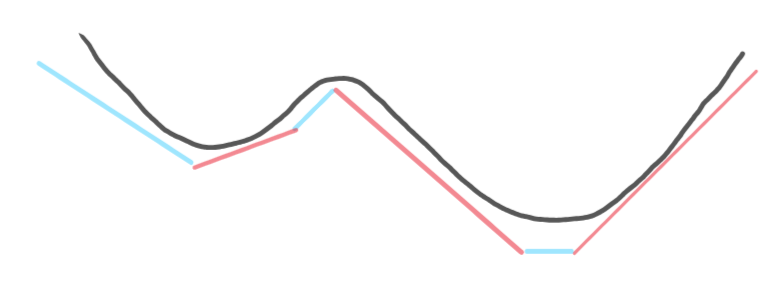
Tropical geometry is an algebraic framework where addition and the maximum operator are its core components. Therefore, in this case, one can naturally represent a neural network as a rational function in this framework. In this paper, we realise this theoretical connection computationally to allow for the effective study of neural networks. In particular, we can exploit the features of the tropical geometry framework to understand the properties of neural networks. Our focus was on expressivity since one can naturally use the tropical representation of the neural networks to determine the regions on which each piece-wise linear component is defined. These regions are known as the linear regions of the neural network and have been established as a metric correlated with the expressivity of the neural network. Our computational methods provide a way to exactly enumerate all of the linear regions of a neural network in its full input space, something that has remained elusive until now.

Furthermore, tropical geometry geometrically characterises these regions, so that we can start asking questions about how their geometry relates to the performance of the network. However, our tools extend beyond just the linear regions of the neural networks, by allowing questions to be asked about the space of neural networks, the compressibility of neural networks and so forth. In our paper, we explore a potential way to investigate the latter.

The tropical geometry representation of a neural network has a certain number of monomials. Loosely speaking, these monomials correspond to one of the linear functions the neural network computes. However, in each region of our input space, our neural network is only considering the maximum linear function out of all the linear functions it is computing. It is plausible that one of these linear functions, or monomials, is never the maximum in any region. Therefore, from the perspective of the final function of the neural network, this monomial is redundant. That is, we could remove it from the tropical geometry representation of the neural network without affecting its performance. Similarly, if the linear function was only the maximum at a point rather than a region, then again we could remove it without affecting the function of the network.

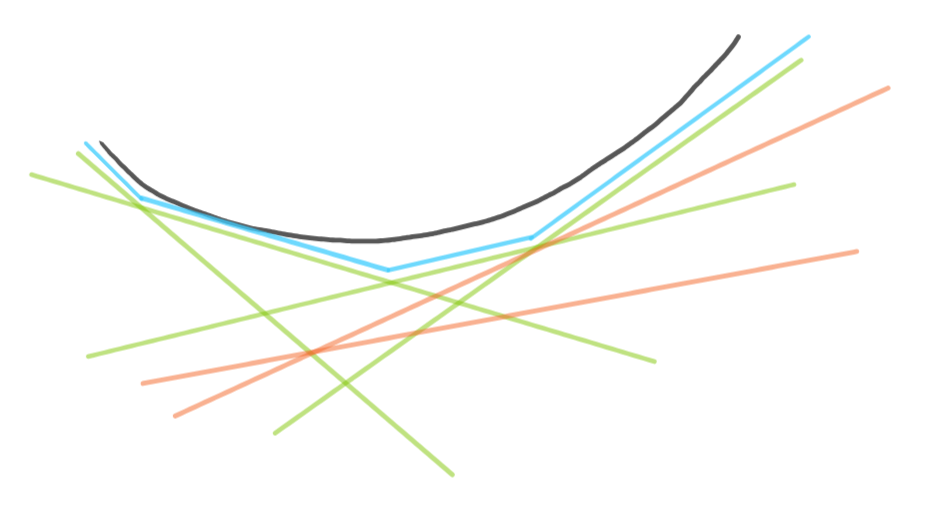
Having access to the monomials through tropical geometry, allows us to effectively identify these occurrences. Understanding how they relate to the absolute architectural instantiation of the neural network would allow for the compression of neural networks without compromising their performance.

In our paper, we explore other consequences of the tropical geometry interpretation of neural networks, including understanding the arrangement of its linear regions and the consequences of its symmetries.