Given a train neural network, DeepDIG [1] is a framework for generating instances along a classification boundary that are as closes as possible to the boundary whilst still being similar to instances of the classes. Given data for the two classes, say a positive and negative class, whose decision boundary you want to investigate, the DeepDIG framework works in three-steps.

1. Train an autoencoder to reconstruct the positive class instances, whilst regularizing the reconstructions to be re-classified as the negative class.
2. Train a second autoencoder to reconstruct the reconstructions of the first autoencoder, however, now regularize the re-reconstructions to be classified as the positive class.
3. Run a binary search algorithm on the a reconstruction from the first autoencoder and its reconstruction under the second encoder to arrive at instance close to the decision boundary.

There is a separate hyper-parameters at steps 1 and 2 which control the extent to which the autoencoder is regularized to change the the classification output of the instance. In practice I find that determining the value of this hyper-parameter is challenging, as the behavior of autonecoders seems to be sensitively dependent on it. Ideally, this hyper-parameter would be as low as possible to ensure the borderline instances remain close to the original instances. However, if it is too low then the instances will not be re-classified by the model, and so the subsequent steps of the DeepDIG framework suffer.

For some simple datasets we observe that DeepDIG can successfully identify instances at the classification boundary between classes.

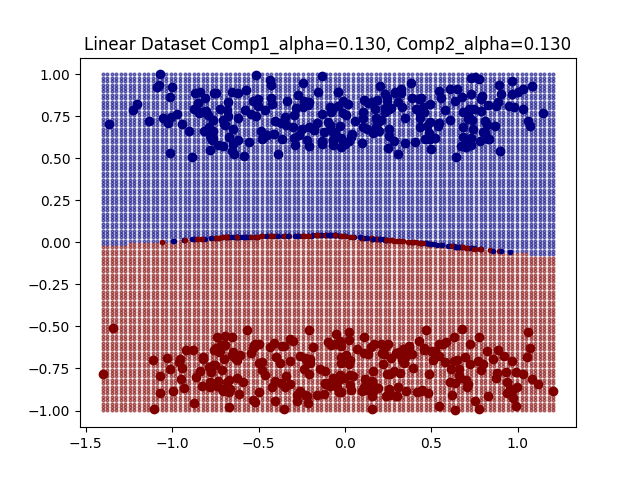
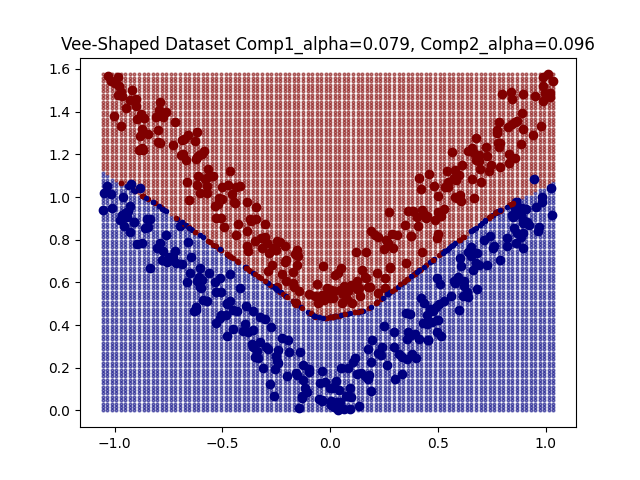
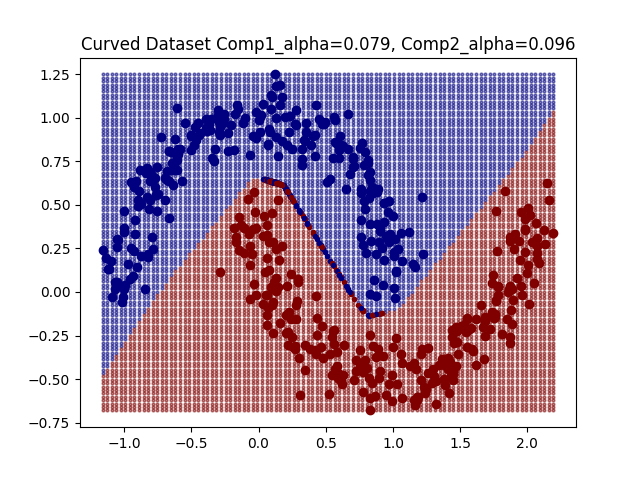
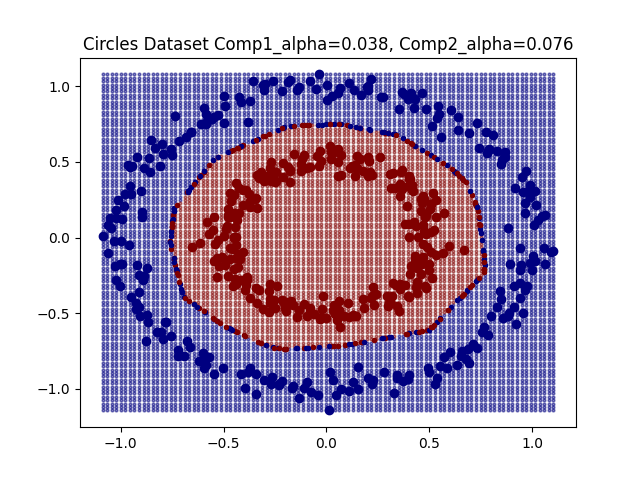
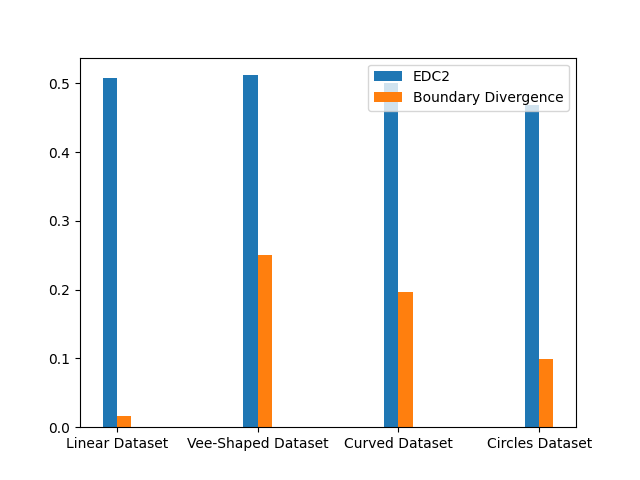
With these identified borderline instances we can investigate the geometry of the classification boundary. In [1] it is suggested to train a linear classifier on the original class instances and then observe its accuracy on the borderline instances. [1] refers to this as the EDC2 metric and suggests that it having a higher value indicates that the decision boundary is more complex. On the other hand, I propose an alternative metric, namely the boundary divergence metric. For this metric we sample points from the bounder line instances, and compute the cosine similarities between the vectors connecting these points. The intuition here is that a linear classification boundary will see many of these cosine similarities be plus or minus one, whereas a more complicated decision boundary may see more cosines similarities concentrated around zero. We perform this random sampling for many points, and observe one minus the average cosine similarity such that a high boundary divergence value corresponds to a more complex decision boundary.

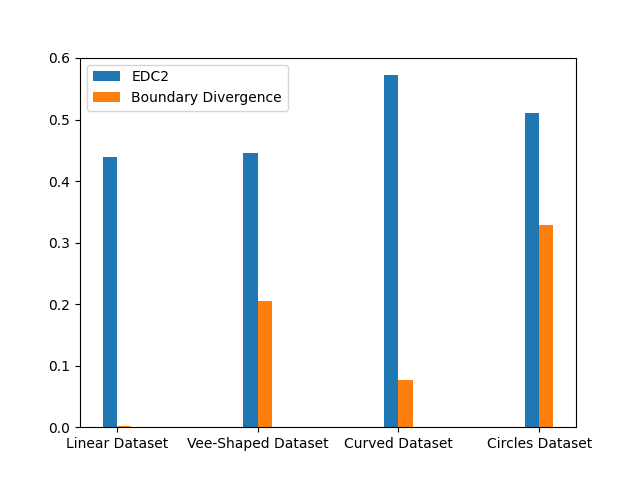
As expected we get boundary metric values that reflect the complexities of the corresponding decision boundaries. However, one observation is that the EDC2 values remain concentrated around 0.5.

The values of these boundary metrics can be significantly influenced by the hyper-parameter selection we discussed earlier. For example, if the hyper-parameter is too large then the borderline instances tend to concentrate. Therefore, one the one hand a linear classifier trained on the original instances will not be reflective of the geometry of the borderline instances as they have diverged too far away from the original instances. On the other hand, if the borderline instances concentrate, then their geometry simplifies and no longer reflect the geometry of the entire boundary.

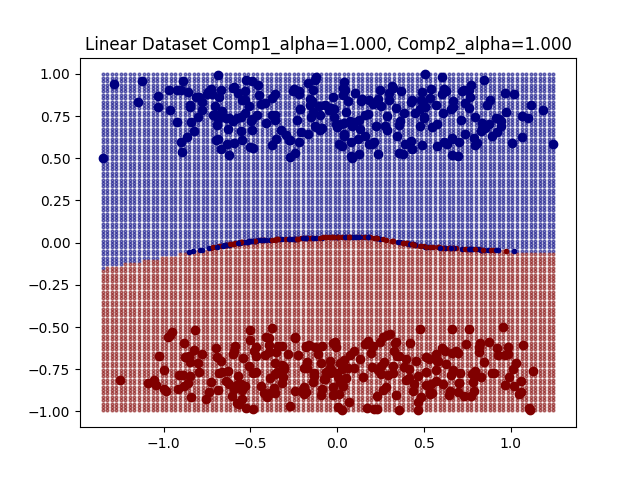
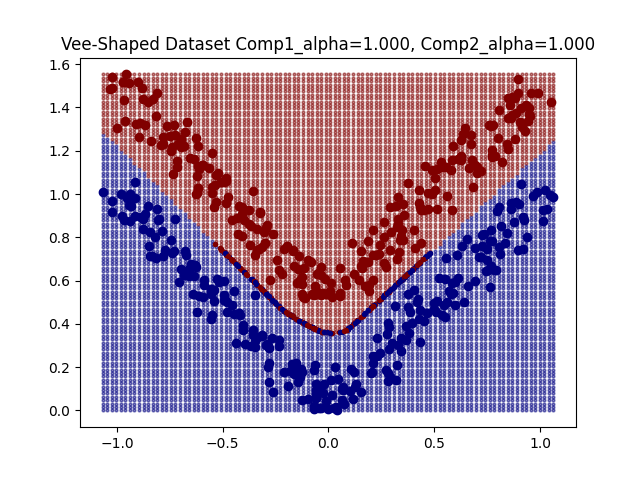
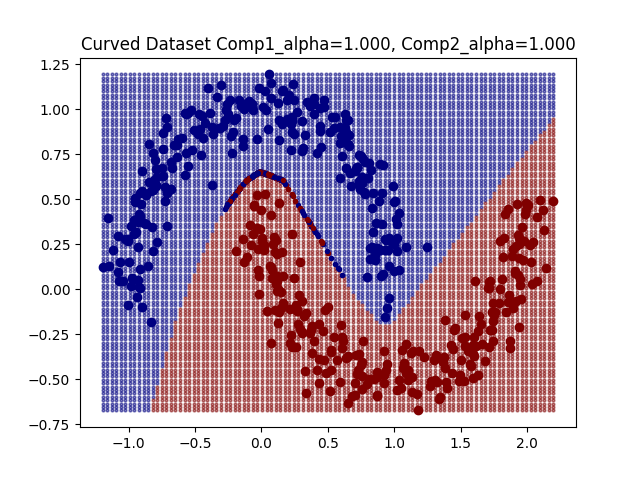
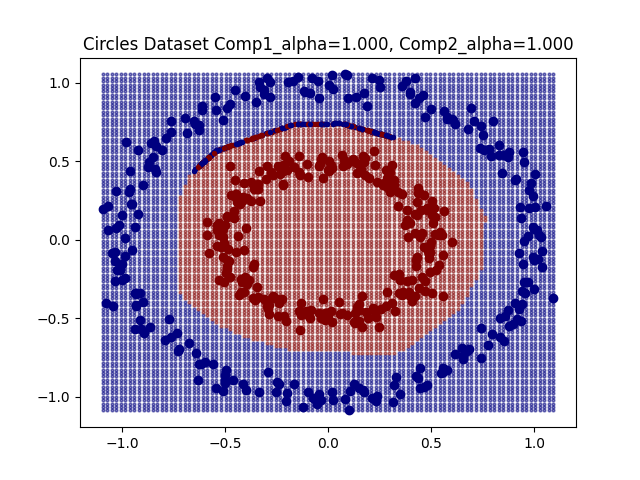
The EDC2 metric seems to concentrate around 0.5, and the boundary divergence metric represents more linear boundaries as the concentration of borderline line instances means that classification boundary looks linear.

References

[1] Karimi, H., Derr, T. and Tang, J. (2020) ‘Characterizing the Decision Boundary of Deep Neural Networks’. arXiv. Available at: https://doi.org/10.48550/arXiv.1912.11460.